La città di Könisberg, nella Prussia Orientale, è situata sul fiume Pregel. Qualche buontempone aveva posto l’oziosa questione se fosse possibile, partendo da un punto qualsiasi della città, ritornarvi dopo aver attraversato una sola volta tutti i sette ponti della città.
Il problema venne risolto dal grande matematico Eulero nel 1736, e la sua soluzione all’indovinello di Könisberg segnò la nascita di due nuove discipline matematiche, la topologia e la teoria dei grafi, offrendo il primo esempio di come un disegno schematico di un problema logico possa essere particolarmente efficace nella soluzione del problema. Eulero si rese conto che si trattava di un problema di geometria che non aveva a che fare con l’effettiva posizione degli oggetti nello spazio, in questo caso i ponti, ma solamente con la loro posizione relativa e di come essi fossero connessi tra loro. Egli considerò la ‘rete’ formata dai quattro luoghi dai quali poteva aver inizio la passeggiata, le due rive del fiume e le due isole (i ‘vertici’ o ‘nodi’ di quello che oggi chiamiamo un ‘grafo’) e dai ponti (i ‘lati’ del grafo): affinché sia possibile attraversare ogni ponte una volta sola, ogni vertice che non sia un punto di partenza o di arrivo deve dare origine a un numero pari di lati, uno per arrivare e uno per allontanarsi. Ma nella rete che rappresenta il problema di Könisberg non ci sono vertici con un numero pari di lati: dunque non è possibile attraversare tutti i ponti una volta sola.
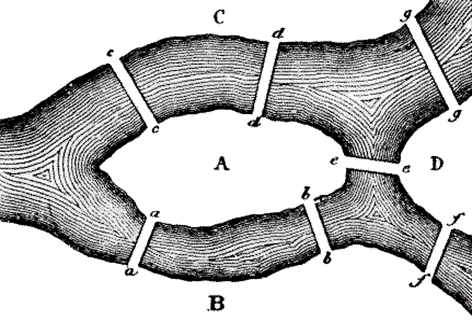

1| Grafo del problema dei sette ponti
La celebre mappa della metropolitana di Londra disegnata da Henry Beck nel 1931 ci dà la ‘struttura topologica’ del sistema e ci offre in un colpo d’occhio tutta l’informazione rilevante per andare da un punto A a un punto B, anche se è totalmente scorretta dal punto di vista geografico. Beck dovette insistere molto perché l’ente pubblico accettasse di pubblicare quella carta, ma il pubblico l’accolse subito molto favorevolmente.
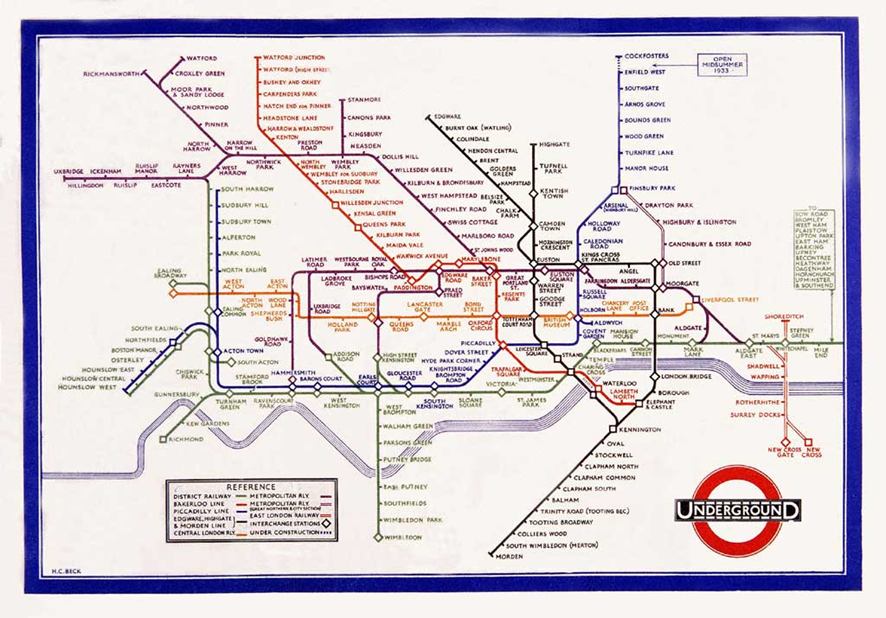
2| La mappa della metropolitana di Londra di H. Beck
Un grafo è un diagramma composto da due tipi di elementi: i ‘vertici’, o ‘nodi’, e i ‘lati’ che uniscono i nodi e che rappresentano delle relazioni fra questi vertici. Se le relazioni sono asimmetriche, i lati sono designati da frecce che indicano la direzione delle relazione e il corrispondente grafo è detto un ‘grafo diretto’; se sono simmetriche, la convenzione è quella di usare semplicemente un segmento senza punte di freccia e il grafo è detto ‘indiretto’. Un ‘percorso’ fra due vertici A e B è una sequenza di lati, senza interruzioni, che connettono A e B passando attraverso altri vertici. L’importanza dei grafi come strumenti di visualizzazione sta soprattutto nella possibilità di rappresentare non solamente relazioni spaziali, ma relazioni di tipo logico o fisico (ad esempio relazioni causali) fra oggetti o concetti.
I primi scienziati che hanno fatto un uso sistematico e importante dei grafi sono stati i biologi. La metafora dell’‘albero della vita’ è antica, ma è con Darwin, e poi con Ernst Haeckel, che conierà il termine ‘filogenesi’, che gli ‘alberi filogenetici’ vengono a rappresentare la relazione di discendenza nella catena evolutiva. Nella terminologia della teoria dei grafi gli ‘alberi’ sono una sottoclasse di grafi nei quali esiste almeno un percorso tra due nodi qualsiasi e tale percorso è l’unico esistente fra questi due nodi.
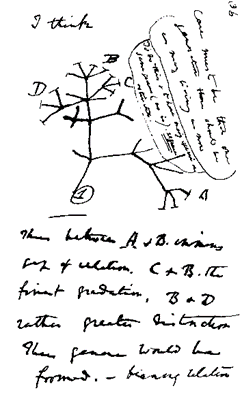
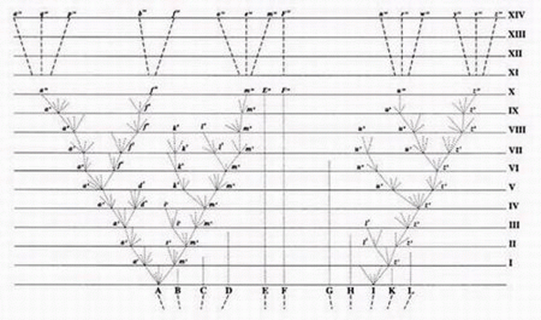
3| Il primo albero della vita disegnato da Darwin in un taccuino del 1837 (a sinistra) e 4| (a destra) l’unica illustrazione de L’origine delle specie (1859)
Un celebre grafo che rappresenta relazioni di influenza concettuale è la mappa disegnata dal direttore del MoMA, Alfred Barr, per il catalogo della mostra Cubism and Abstract Art, nel 1936. Barr faceva uso, come Beck, di alcuni artifici visuali per rappresentare più dimensioni dell’informazione su una superfice bidimensionale: frecce nere e nodi neri per le relazioni di influenza diretta, e frecce rosse e nodi rossi per le relazioni di influenza indiretta; una griglia collocava i nodi in una successione temporale. L’uso di frecce suggeriva, forse non intenzionalmente, l’unidirezionalità della relazione: non veniva graficamente rappresentata l’esistenza di influenze reciproche e la storia dell’arte dei primi trent’anni del novecento appariva perciò come un necessario cammino verso l’astrazione, anticipando la visione che verrà fatta propria dal formalismo di Clement Greenberg.
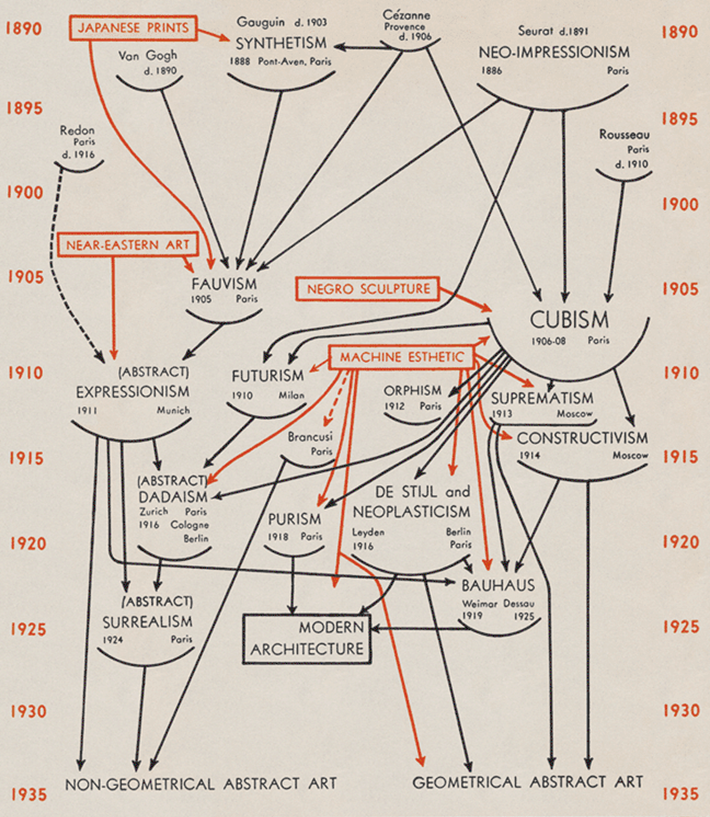
5| La copertina di A. Barr, Cubism and Abstract Art, New York, 1936
Lo storico statunitense dell’arte precolombiana George Kubler ebbe l’idea che l’intera ‘storia delle cose’, l’ininterrotta sequenza degli artefatti, artistici e non, prodotti dall’uomo, potesse essere rappresentata da un grafo diretto che mostrasse “i legami di tradizione e influenza [che] formano una sequenza concatenata” (Kubler [1962] 1976, 44) di “soluzioni” a un problema artistico. Nel suo libro Kubler ricorda come fu un suo collega a Yale, il matematico Oystein Ore, a segnalargli la possibilità di usare una particolare sottoclasse di grafi, i cosiddetti grafi ‘aciclici’, come mappa direzionale e così riporta una nota scritta inviatagli da Ore:
We are concerned with the variety of stages in the creativity of the human race. From one stage one moves to another in the development. There are a variety of directions which may be selected. Some represent actual happenings. Others are only possible steps among many available ones. Similarly each stage may have occurred among several possible steps leading to the same result. This one may picture in a general way by the mathematical concept of a directed graph or network. Such a graph consists of a number of points or vertices or stages. Some of these are connected by a directed line, an edge or a step. At each stage there is therefore a number of alternative edges from which which may be followed, and also a number of incoming edges from which this stage could have resulted. The actual development corresponds to a (directed) path in the graph and it is only one among many possible ones. One may ask whether the graphs we should like to consider are of a special type among the many directed graphs which can be constructed. There seems to be one essential restriction, that the graphs shall be acyclic, that is, there exists no cyclic directed path returning to its original stage. This essentially corresponds to the observation about human progress that it never returns to the previous conditions (Kubler 1962, 33-4, n. 3).
Ci interessiamo alla varietà degli stadi di creatività della razza umana. Nel processo di sviluppo si passa da uno stadio all’altro. Esiste una possibilità di scelta tra numerosissime direzioni. Alcune rappresentano avvenimenti reali. Altre sono soltanto dei passaggi possibili tra i molti che si offrono alla scelta. Così ogni stadio può essersi verificato in più di uno dei passaggi possibili che portano allo stesso risultato. Ciò può essere raffigurato in maniera generale con il concetto matematico di grafico direzionale o reticolare. Un grafico di questo tipo consiste di un certo numero di punti o vertici o stadi. Alcuni di essi sono collegati da una direttiva, un lato o un passaggio. A ogni stadio abbiamo quindi un certo numero di lati alternativi che si possono seguire a partire da quel punto e un certo numero di lati che vengono a terminare in quel punto e dai quali forse è risultato lo stadio in esame. Lo sviluppo reale corrisponde a una linea (direttiva) del grafico, che è soltanto una delle direttive possibili. Si potrebbe porre la questione se tra i molti diagrammi direzionali che si possono costruire quelli che vorremmo considerare siano di un tipo speciale. Una sola limitazione appare in questo senso necessaria: i grafici devono essere aciclici, cioè non devono contenere alcun percorso ciclico che ritorni al punto di partenza. Questa condizione essenziale trova riscontro in quanto è stato osservato nel progresso umano che non ritorna mai a condizioni precedentemente esistite (Kubler [1962] 1976, 44-5, n. 1).
Kubler non disegnò mai un grafo delle sue “sequenze formali”, ma i grafi sono entrati, dagli anni sessanta in poi, nella cassetta degli attrezzi dell’arte post-concettuale. Un esempio di utilizzazione ‘artistica’ dei grafi, sempre per rappresentare relazioni di tipo concettuale, sono le opere dell’americano Mark Lombardi, che ha disegnato una serie di grandi diagrammi con l’intenzione di tracciare le relazioni del potere politico e finanziario nell’era della globalizzazione. Il suo lavoro George W. Bush, Harken Energy and Jackson Stephens, ca 1979–90 del 1999, esposto anche a DOCUMENTA 13 mostra le connessioni di affari tra le famiglie Bush e Bin Laden.
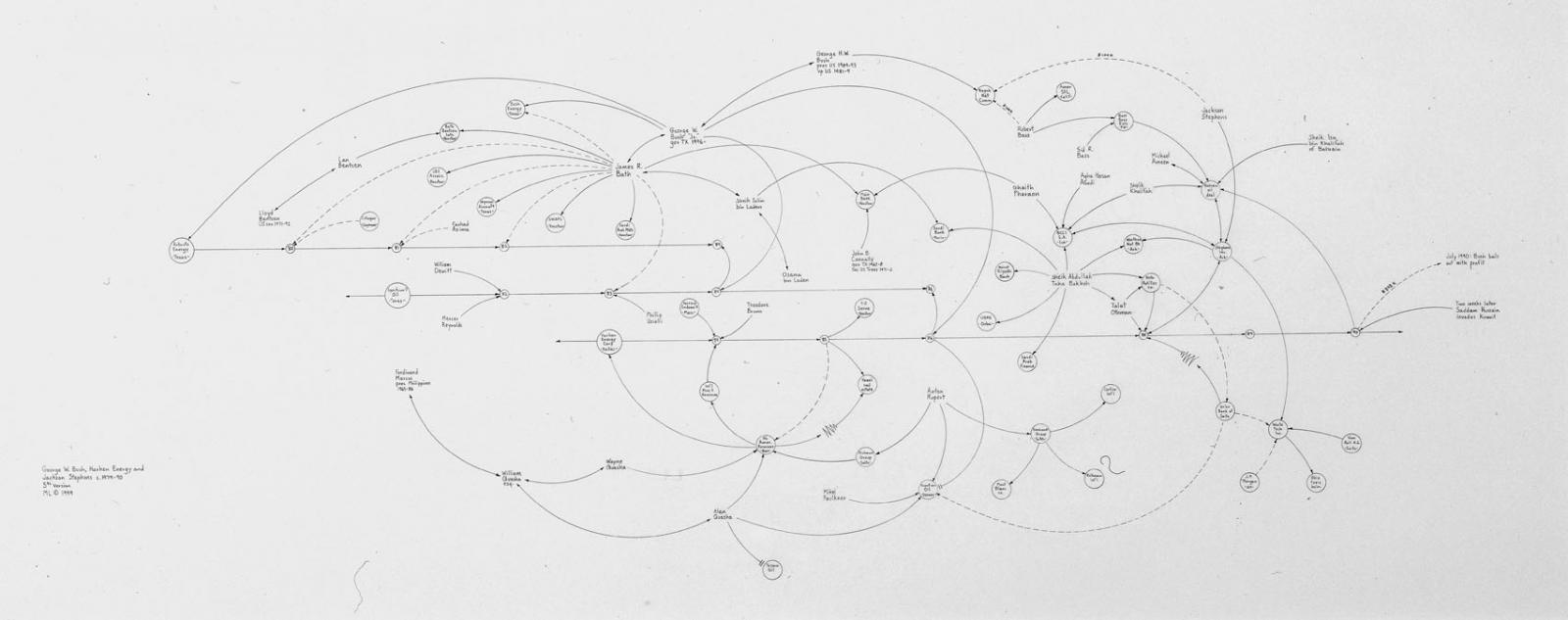
6| M. Lombardi, George W. Bush, Harken Energy and Jackson Stephens, ca 1979–90, grafite su carta (1999)
I lati di un grafo possono rappresentare non solamente generiche relazioni di influenza concettuale o relazioni di tipo fisico, ma anche relazioni di tipo logico e argomentazioni e ragionamenti. All’inizio del Novecento, un professore di diritto americano, John Wigmore, ebbe l’idea di rappresentare il ragionamento probatorio giudiziario sotto forma di diagrammi.
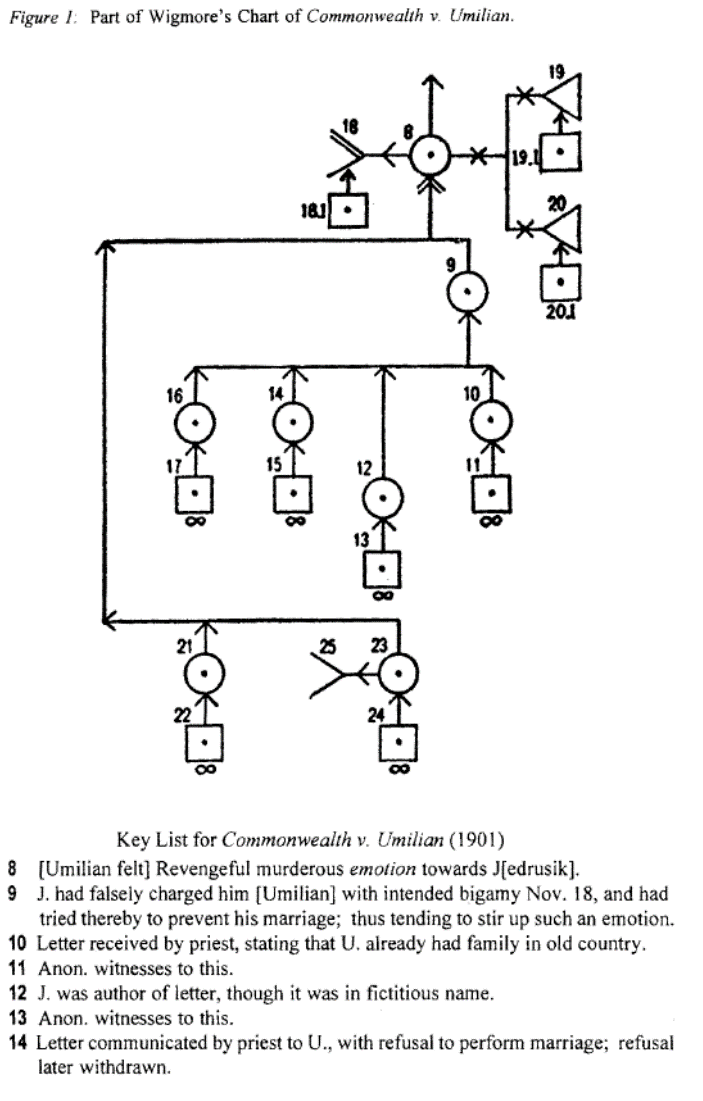
7| Un diagramma di Wigmore, da Goodwin 2001, 226.
Le Wigmore’s Charts (Wigmore 1937) avevano un aspetto piuttosto complicato e vennero dimenticate per molto tempo, fino a quando una convergenza di risultati provenienti dalla teoria dei grafi, dalla logica matematica, dalla fisica, in particolare dalla meccanica statistica, dalla statistica e dall’informatica hanno permesso, negli anni Ottanta del secolo scorso, la nascita delle cosiddette ‘reti bayesiane’. Il nome deriva da Thomas Bayes, matematico del XVIII secolo, il quale formulò per primo il teorema del calcolo delle probabilità che oggi porta il suo nome e che costituisce una delle regole fondamentali del ragionamento probabilistico. Questa regola viene oggi eseguita da programmi informatici per comuni personal computer che permettono di svolgere in pochi secondi inferenze che due secoli fa potevano essere fatte, con lunghi calcoli manuali, solo dai più grandi matematici dell’epoca.
Una rete bayesiana è un grafo aciclico diretto (come i grafi di Kubler) i cui nodi rappresentano proposizioni, o variabili matematiche, e a ciascuno di essi sono associati dei numeri reali, compresi fra 1 (uno) e 0 (zero) inclusi, che misurano la probabilità che la proposizione rappresentata dal nodo sia vera, o che la variabile rappresentata dal nodo abbia un particolare valore.
Un esempio di rete bayesiana è dato nella figura che segue, nella quale i nodi della rete, come ad esempio il nodo indicato da {A, AC }, rappresentano proposizioni del linguaggio. L’esempio è tratto da un libro, scritto da uno statistico e da un esperto di intelligence, che hanno riesaminato tutto il materiale probatorio del celebre caso dei due anarchici italiani condannati a morte negli Stati Uniti il secolo scorso.
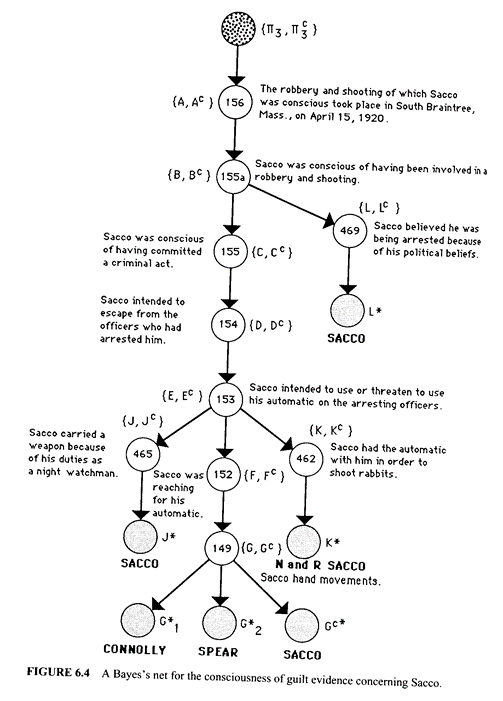
8| Rete bayesiana da Kadane, Schum 1996, 232.
Se la proposizione A è vera, la probabilità è 1 e al suo complemento logico, cioè la negazione di A, nella figura 8 denotato da AC , verrà assegnato automaticamente il valore 0 (e viceversa se, sulla base dell’informazione, la proposizione A è falsa). Se lo status epistemico della proposizione è incerto, allora avrà un valore di probabilità p, compreso fra 1 e 0, e la sua negazione avrà, automaticamente, il valore (1 – p).
Come vengono stimate queste probabilità? La teoria che sta a fondamento delle reti bayesiane ci permette di suddividere problemi complessi, che coinvolgono moltissime proposizioni o variabili, in problemi molto più semplici che coinvolgono un numero molto minore di proposizioni, o variabili, e per i quali siamo in grado di avere informazioni che ci permettono di stimare le probabilità in questione. Il punto fondamentale è che ci sono solamente tre possibili configurazioni elementari di un grafo diretto e qualsiasi grafo diretto, qualunque sia la sua complessità, è costruito da catene composte da queste tre connessioni elementari (A, B e C stanno per tre nodi qualunque del grafo):
connessioni seriali: A → B → C
connessioni divergenti: A ← C → B
connessioni convergenti: A → C ← B
Noi scegliamo quali nodi introdurre, la loro semantica e costruiamo le catene di tutte queste connessioni sulla base di un modello teorico del problema in questione. Il grafo mostra l’‘architettura logica’ del problema, per così dire, e le regole di inferenza e di calcolo sono incorporate nella struttura stessa del grafo. Dopo aver costruito questa ‘mappa’ astratta, per stimare le probabilità necessarie per trasformare il grafo aciclico diretto in una ‘rete bayesiana’, possiamo procedere passo per passo associando a ciascuna freccia nelle connessioni elementari quelle che sono chiamate ‘probabilità condizionate’.
Prendiamo, ad esempio, la connessione seriale (a). Alla freccia che va dal nodo A al nodo B dobbiamo assegnare due probabilità condizionate: (1) la probabilità che la proposizione rappresentata dal nodo B sia vera supposto (a condizione che, da qui il termine ‘probabilità condizionate’) che la proposizione rappresentata dal nodo A è vera; (2) la probabilità che la proposizione rappresentata dal nodo B sia vera, supposto che la proposizione rappresentata dal nodo A è falsa. Tali probabilità possono essere stimate solamente in base alle conoscenze che abbiamo circa la relazione fra A e B, senza preoccuparci né della proposizione C né di tutte le proposizioni che possono stare a monte di A, perché A ‘scherma’ B dall’influenza che possono avere tutte queste altre proposizioni, e B ‘scherma’ A da C. In altri termini, l’influenza che tutte le proposizioni a monte di A possono avere su B passa solamente attraverso lo stato (vero o falso) di A, e l’influenza che C può avere su A passa solamente attraverso lo stato di B. Analogamente succede con la freccia che va da B a C.
Pensiamo, ad esempio, a una sequenza di esperimenti in cui il risultato di ogni esperimento non è indipendente dai risultati degli esperimenti precedenti ma è direttamente dipendente solamente dal risultato dell’esperimento immediatamente precedente a quello considerato: il valore di C allora dipende anche dal valore di A, ma solo indirettamente attraverso l’influenza che A esercita su B. Allo stesso modo, nelle connessioni divergenti e convergenti, C ‘scherma’ A da B e viceversa.
Sarà poi il programma informatico, applicando le regole del calcolo delle probabilità, incluso il teorema di Bayes, a controllare se tutte queste probabilità ‘locali’ siano coerenti fra di loro. Se c’è qualche incoerenza logica nascosta nelle nostre stime, il programma ce lo segnala comunicando anche in quali punti del grafo vi siano incoerenze e pertanto come alcune nostre stime di probabilità ‘locale’ vadano controllate e riviste. Una volta assicurata la coerenza delle probabilità ‘iniziali’, possiamo cambiare le probabilità in qualche punto del grafo, se abbiamo delle nuove informazioni, e il programma automaticamente aggiornerà tutte le altre probabilità in modo logicamente coerente, trasmettendo la nuova informazione a tutti quei nodi del grafo il cui stato è suscettibile di essere modificato da essa, in base alle relazioni fra i nodi che abbiamo. La macchina ‘impara’ dall’esperienza.
La condizione di assenza di cicli nel grafo è essenziale, altrimenti il programma che esegue i calcoli entrerebbe in quello che gli informatici chiamano un loop e si bloccherebbe. Perciò, le reti bayesiane sono adatte a rappresentare catene di implicazioni logiche “se … allora” e inferenze causali in cui vi siano relazioni causa-effetto unidirezionali. In tutti questi casi esse ci permettono di applicare all’analisi di problemi complessi l’aurea massima degli antichi Romani: divide et impera.
Nella loro semplicità, queste tre connessioni elementari rappresentano tre modi fondamentali del buon ragionamento, sia scientifico che di senso comune.
Una ‘connessione seriale’ (a) rappresenta ciò che si chiama un ‘processo a catena di Markov’. Il nome deriva dal matematico russo Andrei Markov (1856-1922) e i ‘processi markoviani’ si ritrovano in moltissimi fenomeni nei più svariati campi, dalla fisica alla sociologia, dalla biologia all’ingegneria. Una ‘catena di Markov’ costituisce l’esempio più semplice di quella proprietà fondamentale di ‘schermatura’ di cui godono le reti bayesiane e della quale abbiamo parlato sopra e, per questa ragione, tale proprietà viene chiamata proprio la ‘proprietà markoviana’.
La ‘connessione divergente’ (b) rappresenta un principio di grande importanza non solo per il ragionamento, il cosiddetto ‘principio di causa comune’, formulato dal filosofo della scienza Hans Reichenbach (Reinchenbach 1956). Il perché del nome è intuitivo (C influenza sia A che B, ma non viceversa) ma, nella sua apparente semplicità, il principio sta nel cuore del problema della direzione del tempo, perché tutte le connessioni divergenti che conosciamo sono dirette verso il futuro e nessuna verso il passato (Rovelli 2017, 143-146). Inoltre esso guida una prassi fondamentale delle indagini statistiche. Due eventi A e B possono esibire una correlazione statistica senza che A sia causa di B né che B sia causa di A, perché entrambi i fenomeni sono, in realtà, effetti di una causa comune C. Qualora si sospetti che la correlazione fra due fenomeni non sia indice di una genuina relazione causale fra di essi, ma dipenda dalla comune dipendenza da un terzo evento, occorre eseguire delle osservazioni nelle quali il valore della ipotetica causa comune C viene tenuto fisso, il ‘valore di verità’, nel caso C sia una variabile proposizionale, il valore numerico nel caso C sia una variabile quantitativa: se i valori di A e B risultano indipendenti fra di loro quando il valore di C è tenuto fisso, allora A e B sono effetti comuni di C. Ad esempio, nelle indagini epidemiologiche come possiamo controllare se B sia effettivamente un fattore causale di A e non sia un effetto collaterale del vero fattore causale C? Cercheremo di effettuare due serie di osservazioni, in una delle quali abbiamo A, C e B e nell’altra abbiamo A e C, ma non B: se la frequenza di A nelle due serie non varia in maniera significativa, allora A non dipende da B. E viceversa se, invece, la frequenza di A variasse in maniera significativa.
Una ‘connessione convergente’ (c) permette di rappresentare un’altra sofisticata forma di ragionamento che occorre quando si ritiene che A e B siano indipendenti fra di loro ma entrambi rilevanti per C. Un esempio di questa situazione può essere dato nel campo del ragionamento probatorio giuridico. Sia A la proposizione ‘il sospettato ha commesso il fatto’, B la proposizione ‘la traccia trovata sul luogo dove è stato commesso il fatto è stata lasciata da colui che ha commesso il fatto’, e C la proposizione ‘il sospettato è l’origine della traccia trovata sul luogo dove è stato commesso il fatto’. Il nodo B rappresenta l’ipotesi circa la rilevanza della traccia trovata, cioè se la traccia sia veramente collegata al fatto indagato oppure sia stata prodotta in altre circostanze. Se non sappiamo se C sia vera, allora sapere che A o B sia vera non fornisce alcuna indicazione circa la verità dell’altra: l’informazione che la traccia provenga da colui che ha commesso il fatto non ha alcuna rilevanza, presa di per sé, per l’ipotesi che il sospettato abbia commesso il fatto e, viceversa, che il sospettato abbia commesso il fatto non influenza la rilevanza della traccia trovata sulla scena del delitto, che dipenderà dalla sua posizione, dalla sua freschezza, e da altri parametri che non dipendono dalla particolare persona che ha effettivamente commesso il fatto. Ma se ipotizziamo, o sappiamo, che sia vero che il sospettato è l’origine della traccia, allora A e B sono tra loro logicamente dipendenti: se è vero che la traccia è stata lasciata da colui che ha commesso il fatto e se è vero che il sospettato ha lasciato la traccia, allora è vero che il sospettato ha commesso il fatto.
Se è solamente probabile (con un valore di probabilità p inferiore a 1) che la traccia sia stata lasciata da colui che ha commesso il fatto (perché è possibile che la traccia non sia collegata al fatto o che il sospettato abbia lasciato la traccia in circostanze diverse) e se è solamente probabile (con un valore di probabilità q inferiore a 1) che la traccia sia stata lasciata dal sospettato (perché anche la prova del DNA non può assicurare una probabilità di identificazione q pari al 100%), quale sarà la probabilità r che il sospettato abbia commesso il fatto? Ovviamente, dipenderà dai valori p e q, ma come si calcola il valore, anche solo approssimato, di r? Per il ragionamento di senso comune non è facile dare a questa domanda una risposta logicamente corretta ed è in passaggi come questo che le reti bayesiane mostrano la loro utilità.
Le reti bayesiane sono oggi applicate in moltissimi campi, dagli algoritmi di ricerca che impiegano l’analisi semantica al machine learning e alla ricostruzione di immagini digitali, dall’analisi dei rischi in ingegneria alla teoria delle decisioni, dalla diagnosi medica all’inferenza forense, dalla biologia computazionale alla bioinformatica e, naturalmente, in statistica. Ad esempio, la rete bayesiana (mostrata in Fig. 8) serve per la valutazione di una coincidenza fra il profilo del DNA di un sospettato e un profilo conservato in una banca di dati del DNA.
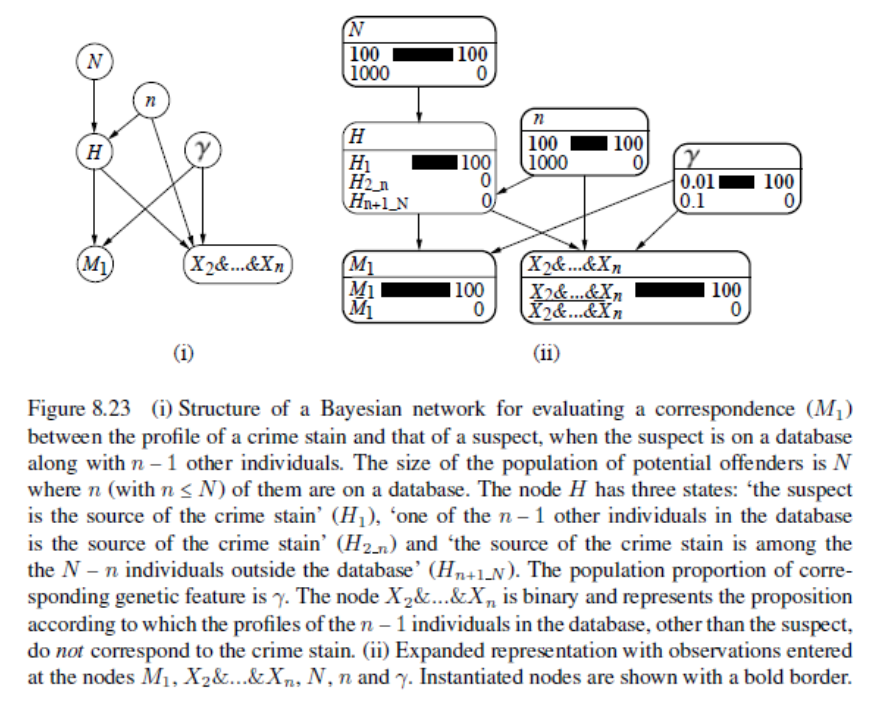
9| Rete bayesiana da Taroni, Biedermann, Bozza, Garbolino, Aitken, 2014, 240.
Le reti bayesiane hanno permesso di realizzare, almeno per quella classe di problemi per i quali sia possibile costruire una base dei dati sotto forma di un grafo aciclico diretto e che non siano computazionalmente intrattabili, quello che il matematico Giuseppe Peano, maestro di Bertrand Russell, chiamò poco più di un secolo fa “il sogno di Leibniz”: riuscire a trasformare “l’arte di valutare le verosimiglianze” (Leibniz [1765] 1982, 361) in un calcolo logico eseguibile da un algoritmo.
Prima di mettere la parola fine, soddisfiamo quei lettori che, forse, saranno rimasti curiosi di conoscere le conclusioni dell’analisi bayesiana del caso Sacco e Vanzetti:
To put a final point on our case study, we suppose that there are readers who, having examined our probabilistic judgments in Chapter 6, will argue that we have provided some cunning ways for hedging a conclusion in probabilistic terms without providing any verdict, as trial jurors are required to do. To answer these persons, we draw upon an element of Scots law. In criminal cases in Scotland, jurors have three options as far as their verdicts are concerned: they can vote guilty, innocent, or, as an intermediate option, not proven. Asked to render a verdict as far as Sacco and Vanzetti are concerned, our vote would be Vanzetti: innocent; Sacco: not proven (Kadane, Schum, 1996, 283).
Arrivati alla fine a questo caso-studio, possiamo immaginare che ci siano dei lettori i quali potrebbero osservare che abbiamo offerto dei modi sottili per evadere la questione mettendola in termini probabilistici, senza emettere un verdetto, cosa che i giurati di un processo devono invece fare. Per rispondere a queste persone, faremo appello alla legislazione vigente in Scozia. Nei processi criminali in Scozia, i giurati hanno a disposizione tre opzioni per il loro verdetto: possono votare innocente, colpevole oppure, come opzione intermedia, assolto per insufficienza di prove. Se ci venisse richiesto un verdetto sul caso di Sacco e Vanzetti, il nostro voto sarebbe Vanzetti: innocente; Sacco: assolto per insufficienza di prove.
Bibliografia
- Barr 1936
A. Barr, Cubism and Abstract Art, New York, 1936. - Rovelli 2017
C. Rovelli, L’ordine del tempo, Milano, 2017. - Goodwin 2001
J. Goodwin, Wigmore’s chart method, “Informal Logic”, 3 (20) (2001), 223-34. - Kadane, Schum 1996
J. B. Kadane, D. A. Schum, A Probabilistic Analysis of the Sacco and Vanzetti Evidence, New York, 1996. - Kubòer [1962] 1976
G. Kubler, La forma del tempo. La storia dell’arte e la forma delle cose [The Shape of Time, Remarks on the History of Things, New Haven 1962], tr. it. di G. Casatello, Torino 1976. - Leibniz [1765] 1982
G. W. Leibniz, Nuovi saggi sull’intelletto umano [Nouveaux essais sur l’entendement humain, Amsterdam et Leipzig, 1765], tr. it. di M.Mugnai, Roma 1982. - Reichenbach 1956
H. Reichenbach, The Direction of Time, Berkeley-Los Angeles, 1956. - Taroni, Biedermann, Bozza, Garbolino, Aitken 2014
F. Taroni, A. Biedermann, S. Bozza, P. Garbolino, C. Aitken, Bayesian networks for probabilistic inference and decision analysis in forensic science, Chichester, 2014. - Wigmore 1937
J. Wigmore, The Science of Judicial Proof: as Given by Logic, Psychology, and General Experience and Illustrated in Judicial Trials, Boston, 1937.
English abstract
Drawings and sketches representing reasoning processes or links between concepts or images have always been widely used. The mathematical theory of graphs, born in the 18th century with Euler, along with the developments of artificial intelligence in the 20th century, offers today the possibility to draw diagrams that visually represent schemes of inferences and incorporate algorithms capable of performing complex logical calculations: Bayesian networks.
keywords | Euler; Könisberg; MoMA’s Cubism; Abstract Art.
Per citare questo articolo / To cite this article: P. Garbolino, Mappe logiche, “La Rivista di Engramma” n. 150 vol. 1, ottobre 2017, pp. 611-623 | PDF