
1 | La Scuola di Matematica vista dall’ingresso dell’aula magna di Chimica, ca. 1935. Foto Cartoni, FRP, BST, UniFi, sezione fotografie, busta 87, 87.22.
Le vere opere somme delle architetture antiche […] sono invenzioni formali e strutturali, sono essenziali, rappresentative, espressive in tutti i loro particolari, sono illusive, perpetue – vi sarà facile identificare l’invenzione formale e strutturale – vi sarà facile vedere l’essenzialità, l’unità e la forma finita – vi sarà facile riconoscere la palese rappresentatività; “sentendo” che una architettura è leggera, ed un’altra è potente, ed un’altra si slancia verso l’alto ne comprenderete l’illusività; dal valore autonomo fuori del tempo di queste opere ne comprenderete la perennità – applicate questi termini di giudizio ad opere moderne (Ronchamp, la “casa sulla cascata”) vedrete voi stessi che rispondono: sono invenzioni, sono essenziali, sono rappresentative di quel che sono, sono espressive in tutti i loro particolari, sono illusive (hanno una ‘loro’ dimensione), sono perpetue (irripetibili) (Ponti [1957], 2010, 71).
In questa dichiarazione tratta da Amate l’Architettura Ponti esplicita il ruolo che gioca l’invenzione nel determinare il valore perpetuo delle opere, in particolare di quelle che costituiscono una “lezione di architettura”.
La Scuola di Matematica [Fig. 1] realizzata per la Città Universitaria di Roma tra 1932 e 1935 ambisce sin dalla sua concezione a collocarsi tra queste “opere perpetue” e non è un caso che negli ultimi anni, forse anche per merito di una nuova coscienza verso il Moderno, l’interesse, gli studi e la curiosità nei suoi confronti siano aumentati, tuttavia proprio in quanto perpetuo questo esempio ha ancora molto da insegnarci. Sulla reputazione di questo edificio ha a lungo pesato la colpa di appartenere al periodo fascista: senza dubbio Zevi ha storicamente influenzato la critica postbellica in senso negativo pur riconoscendone le qualità architettoniche (v. sul tema la ricostruzione di Salvo 2015, 191). Da allora l’atteggiamento verso questo tipo di architettura è cambiato e negli ultimi decenni si sono intensificati studi che per lo più riguardano il campo del restauro (si ricordino in particolare l’intervento di Bardati 2003, 175-181, e il contributo di Mornati 2002, 43-71, che ha messo in luce alcuni aspetti costruttivi di cruciale importanza).
Ciò che qui ci si propone di fare (avvalendosi anche degli esiti della ricerca di dottorato sulla moderna Sapienza da me condotta e confluiti nella pubblicazione La Città Universitaria di Roma. Costruzione di un testo architettonico, Milano 2019) è ricostruire la cornice architettonica entro cui si muovono i ragionamenti formali e spaziali dichiarati e sottesi, ragionamenti che si possono cogliere ripercorrendo idealmente l’opera secondo la sua concezione originaria più che per come si presenta oggi, fatto di per sé sufficiente a giustificarne una rilettura.
L’allora direttore amministrativo dell’Università ricordava che Ponti all’epoca dell’incarico, pur senza alcuna esperienza in merito agli edifici per l’educazione, era riconosciuto “studioso acuto di ogni problema di architettura, felice per ingegnose soluzioni” (Spano 1935, 302), caratteristica che si sommava alla pluriennale pratica nei progetti di residenze, alle frequenti incursioni nel mondo della pittura, dell’artigianato e del disegno industriale, oltre all’impegno profuso nelle Triennali e nella redazione della rivista “Domus”, aspetti che lo rendevano evidentemente il personaggio più adatto a realizzare uno degli edifici più impegnativi del complesso. Una scuola che nasceva dall’intesa dello stesso Ponti con l’architetto capo Marcello Piacentini e con due tra i docenti più lungimiranti, Guido Castelnuovo e Enrico Bompiani, (Mornati 2002, 56, Mornati 2020, 92) entrambi intenzionati a promuovere un’istituzione d’avanguardia, impresa che di fatto si presentava occasione certa di sperimentazione progettuale.
Il programma e la tripartizione; autonomia delle parti e composizione unificante

2 | La piazza della Minerva con gli edifici di Ponti e Michelucci, 1936. “Quaderni della Triennale”, ottobre 1936.
Schema planimetrico della piazza della Minerva, in rosso sono evidenziati i sistemi di accesso contrapposti di Matematica e Mineralogia (disegno di G. Baratelli).

3 | G. Ponti, Scuola di Matematica, corte interna, ca. 1935. Foto Vasari, FRP, BST, UniFi, sez. fotografie, busta 87, 87.23.
La scuola che si trova alla destra del Rettorato in contrappunto all’Istituto di Mineralogia occupa la propaggine est della piazza centrale della Minerva, un terminale significativo della pianta basilicale che Piacentini ha predisposto per la nuova Sapienza (Piacentini 1935, 6). Tutta la composizione risente di questa particolarità, uno “sbilanciamento apparente” che se planimetricamente ribadisce la nota conformazione di piazza Navona – presa volutamente a modello nelle proporzioni allungate di 1:6 (Baratelli 2019, 75) – dal punto di vista volumetrico dà luogo ad una attenta ponderazione di masse dove i due blocchi di Michelucci e Ponti si fronteggiano come quinte urbane adottando una logica inversa nel rapporto tra pieni e vuoti dei fronti: il primo con i due accessi simmetrici (alti portali che conducono agli atrii di Mineralogia e Geologia), l’altro che ingloba ingresso e biblioteca in un’unica “spaccatura” centrale [Fig. 2]. Al contrario degli istituti che costituiscono il cuore della cittadella, quasi tutti conformati secondo sagome pseudo quadrangolari intorno a corti più o meno permeabili e diversamente da quanto la vista dalla piazza lascerebbe presagire, quello di Matematica è l’unico edificio dall’impianto dichiaratamente curvo e richiuso su sé stesso.
Proprio percorrendone in continuità il perimetro, ci si accorge che ciò che più sconvolge la sintassi paratattica di cui gode l’equilibrio generale del complesso si deve a una sorprendente e articolata giustapposizione volumetrica che in parte trova giustificazione nella prassi tipica del Ponti di quegli anni di procedere per addizione di parti e per elementi conclusi combinando il rigore di un impianto classico, compiuto, perfettamente simmetrico e in qualche modo anche “solido”, con le necessità di un programma funzionale alquanto denso che presuppone ricerca di forme nuove compatibili con l’uso.
Le richieste del grande matematico Enrico Castelnuovo prevedevano in un sommario elenco iniziale alcune dotazioni essenziali: aule piccole, medie e mediamente grandi distinte per i due cicli di studi e per i corsi ordinari, sale dedicate al disegno, due auditori per 300 studenti, stanze per i professori e abitazione del custode oltre ad una grande biblioteca per circa 75.000 volumi addirittura estensibile a 100.000 (Lettera del professor Guido Castelnuovo al Rettore, 30 marzo 1932, UNIRM1, CERUR, busta 44). Ma nell’opera realizzata gli ambienti destinati ad Aula magna diventano quattro (Architettura 1935, 45-50) e la loro capienza raggiunge le 450 persone, una contingenza plausibilmente verificatasi per errate previsioni di crescita della popolazione studentesca che potrebbe in parte aver influito sulla concezione generale della scuola. L’insieme consta di tre grandi blocchi di altezza e impronta diverse che rinserrano il vuoto centrale di una corte interna: il parallelepipedo dell’atrio e della biblioteca, il corpo a ferro di cavallo delle aule da disegno e la porzione cilindrica che contiene i grandi auditori. Il principale vantaggio di questa modalità aggregativa è la differenziazione caratteriale delle parti che consente di distinguere a colpo d’occhio la testata aulica sulla piazza della Minerva rispetto ai fianchi e a un retro dove l’aspetto funzionale prevale ed è volutamente dichiarato in termini di forma e immagine.
Il sistema pur basato sull’integrazione di volumi diversi, consente anche una certa continuità fruitiva; in questo “Giano bifronte” si entra quasi in sordina accolti da un atrio quadrangolare fiancheggiato da piccole aule, da qui un’alta apertura lascia intravedere il centro, una corte lastricata a opus incertum che nella spazialità e in alcune allusioni figurative richiama l’atmosfera della piazza italiana e dei suoi elementi principali: il palazzo (la biblioteca), i portici (le aule da disegno), il teatro (la torre delle grandi aule). Il flusso della circolazione intorno alla corte non si interrompe mai; un anello centrale collega tutti gli ambienti e quattro accessi laterali arretrati, compressi da corpi più bassi che come cerniere, nell’equilibrio generale della composizione, sottolineano la potenza espressiva delle singole parti [Fig. 3].
La torre delle aule: una spazialità sospesa
Ancora nel 1957 in Amate l’Architettura Ponti, proprio mentre stava realizzando il Grattacielo Pirelli, menzionava tra le sue invenzioni più felici la torre di Matematica (Ponti [1957] 2010, 56) e non è un caso se le grandi aule, così come il loro innesto nell’impianto a U, costituiscono un particolare nodo che l’autore elabora in corso d’opera. Nella prima versione pubblicata su “Architettura” del 1933 (Cerutti Fusco 2003, 111) il corpo di ingresso è costretto tra due patii esterni, un unico centro di curvatura accomuna le circonferenze delle aule da disegno ed il terminale degli auditori; in quella finale la larghezza del fronte si riduce alla sola biblioteca, un secondo atrio si apre verso gli auditori e subentra una variazione sostanziale – lo sdoppiamento del centro di curvatura.
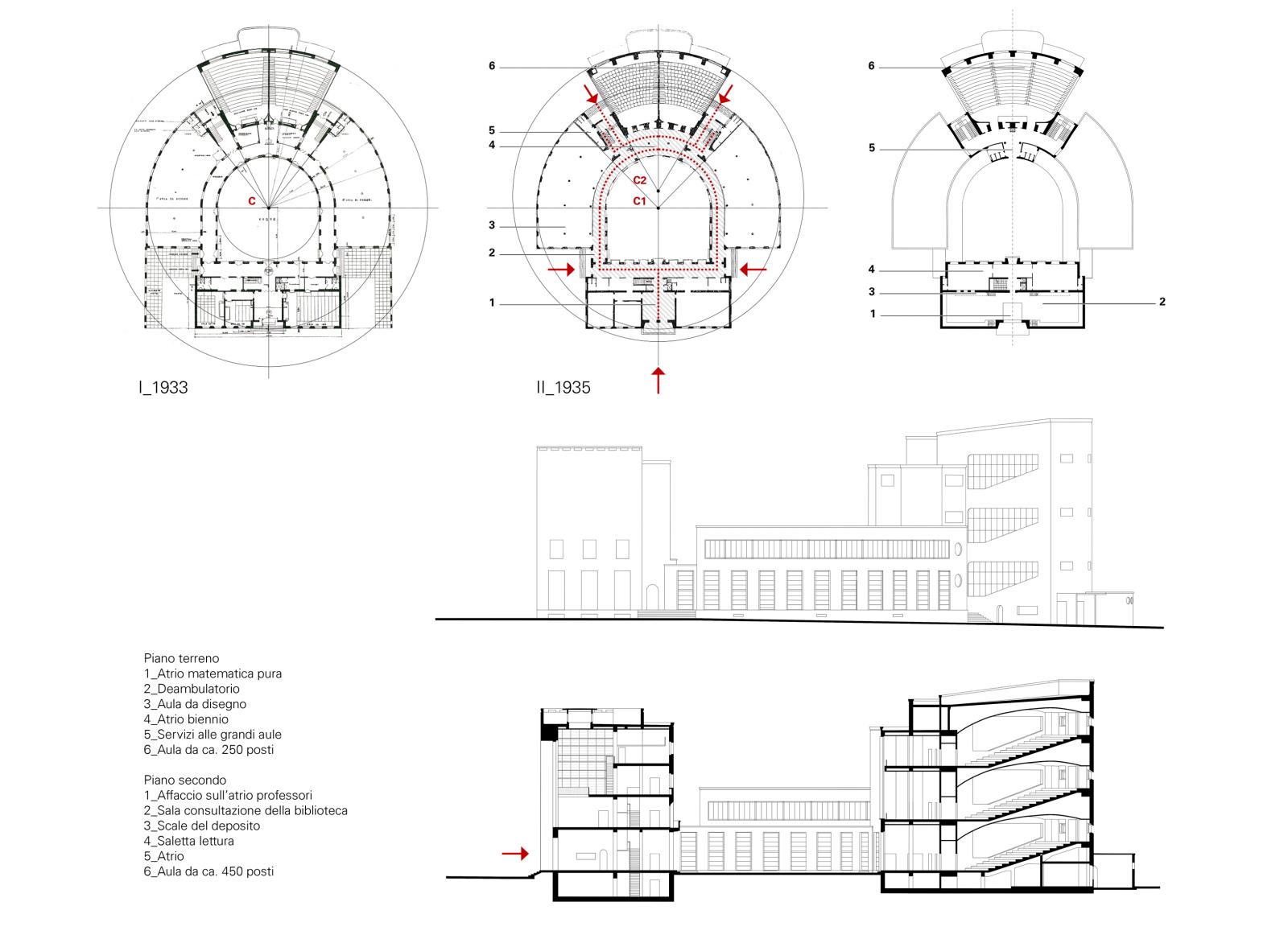
4 | Scuola di Matematica, elaborato di sintesi, genesi geometrica del progetto nelle due principali fasi costruttive 1933 e 1935 (a sinistra in alto), in rosso sono evidenziati il sistema dei percorsi e i diversi centri di curvatura; (a destra) pianta del piano terra e del piano secondo, prospetto laterale e sezione longitudinale dell’istituto, ricostruzione al 1935 (disegno di G. Baratelli).
Sappiamo che tra il 1933 e il 1934 sono state apportate diverse modifiche in cantiere che hanno riguardato la struttura nel passaggio da una costruzione in parte muraria ad una totalmente a scheletro così come la geometria (Lettera della Commissione tecnica di revisione dei progetti e collaudo al Consorzio, 2 dicembre 1933, UNIRM1, CERUR, busta 15, fasc. 144, Cartella Ferrobeton (I), che conferma la natura sperimentale del cantiere). Nella seconda versione planimetrica la diversa impostazione che prevede l’eccentricità lungo lo stesso asse non sembra essere un capriccio dettato da giochi formali ma una scelta estremamente funzionale che a parità di capienza delle sale fa sì che la conformazione delle scale laterali si mantenga regolare costituendo il tramite retto tra i due sistemi di curvatura e facilitando l’inserimento di ulteriori vani di servizio. Anche il muro che separa gli auditori da un secondo atrio si arricchisce di un valore funzionale trasformandosi in un doppio diaframma cavo i cui spazi interstiziali articolati in concamerazioni concavo-convesse comunicano con l’esterno isolando perfettamente le sale (Baratelli 2019, 128-130) [Fig. 4].
L’invenzione vera e propria è nascosta però nella sezione; come ricordava Piacentini:
La struttura, già prevista in cemento armato è molto complessa, sia nelle aule da disegno che, in modo specialissimo, nelle grandi aule da lezione. Per queste ultime l’architetto Ponti ha escogitato una soluzione veramente originale per cui la copertura della sala inferiore costituita da una superficie curva, studiata per la migliore acustica, si inserisce nel vuoto restante sotto i gradini dell’aula superiore, logicamente disposti per la migliore visibilità (Lettera da Piacentini al Consorzio del 1 febbraio 1934, UNIRM1, CERUR, busta 4, fasc. 43).
Il dispositivo aula in effetti si basa su un principio di complementarietà o di incastro che all’intradosso di una sala fa corrispondere l’estradosso dell’altra anche in virtù di un sistema a telaio che copre la considerevole luce di 17 metri senza appoggi intermedi (Poretti 2008, 21-22), un’innovazione non solo strutturale ma anche compositiva.
In quegli anni la cosiddetta torre delle aule deve aver suscitato grande curiosità anche perché ad essa potevano essere paragonati solo pochi modelli di architetture particolarmente sofisticati come la New School for social research di New York e – molto più simile nella concezione dello scheletro e visionaria – la soluzione proposta da Adalberto Libera nel 1934 in occasione del Concorso per il Palazzo del Littorio.
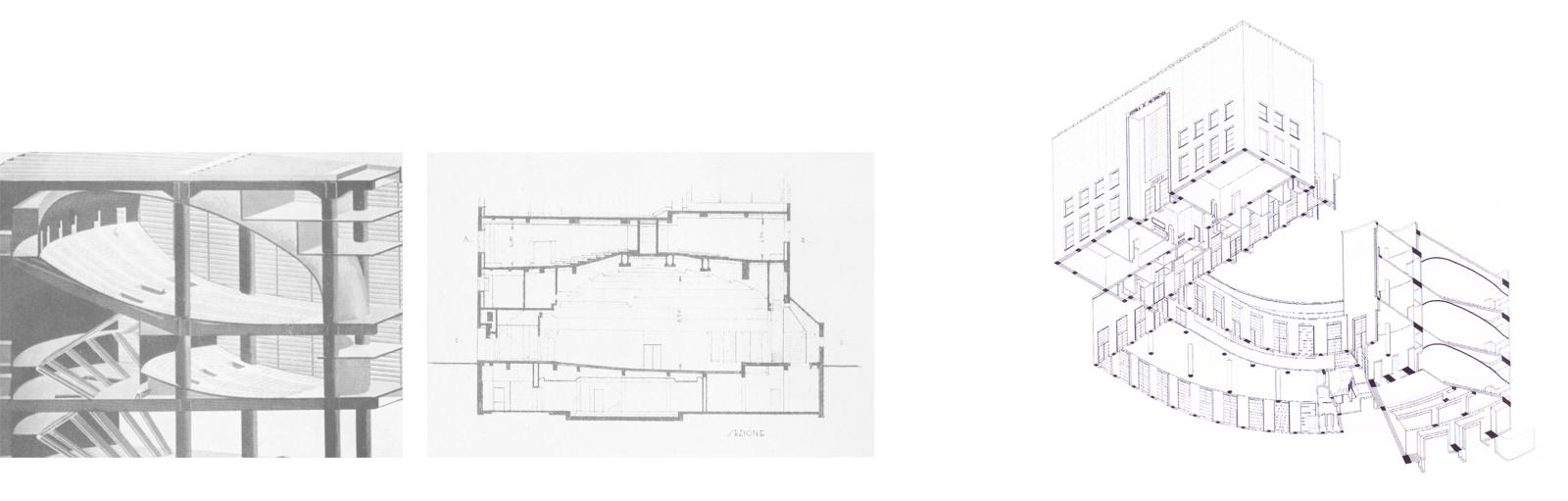
5 | A. Libera, Progetto per il concorso del Palazzo Littorio, assonometria delle aule, 1934. “Architettura”, speciale, 1934.
Piante e sezione delle aule della New School for social research, New York, 1931. G. Minnucci, Degli edifici per l’istruzione superiore: Relazione dell’Ufficio Tecnico per la costruzione della città Universitaria di Roma, Roma, 1932.
Scuola di Matematica, spaccato assonometrico. Disegno di S. Mornati, S. Poretti, Modernismi italiani, architettura e costruzione nel Novecento, Roma, 2008.
In effetti l’interesse che Ponti dichiara per Libera su “Stile” nel 1942, seppur tardivo, rivela alcune affinità di pensiero tra cui, come ha sottolineato Giorgio Ciucci, la ricerca, anche se con linguaggi completamente diversi, di forme strutturalmente pulite, geometriche e ritmiche, di “un’idea-forma capace di racchiudere in sé soluzioni plastiche di ordinarle, controllarle, organizzarle, fino a renderle funzionali” (Ciucci 1989, 62-79) – principi che evidentemente già appartengono a quell’atteggiamento di “rifiuto di forme morte” a cui Ponti allude descrivendo il cambiamento di registro nelle sue architetture a partire dagli anni Trenta (Ponti [1957] 2010, 49-55) [Fig. 5].
La sintesi strutturale a cui in questo caso approda anche grazie all’apporto tecnico dell’ingegner Zadra (Mornati 2002,62) e di Gaetano Minnucci – che cura direttamente l’acustica delle aule nonché tutti i problemi di curvatura che ne derivano – (Pacini 1933, 482), rientra comunque in una intenzione estetica e in un’idea di modernità che l’architetto va maturando nel tempo; modernità che ammette sempre deviazioni di percorso nutrendosi anche di immagini contrastanti e, nel caso specifico, esprimendosi sinteticamente in una “nudità strutturale che, se anche è ostentata, non è priva di grazia” come lo stesso autore già nel 1929 va scrivendo su “Domus” a proposito di una particolarissima scala elicoidale di Robert Mallet-Stevens (Ponti 1929, 38).

6 | Scuola di Matematica, una delle grandi aule da 450 posti e retro della Torre delle aule. “Architettura”, numero speciale, 1935.
Del resto alla struttura corrisponde un’innegabile eleganza interna: il soffitto molto ribassato avvolge l’ambiente dell’auditorio e crea con la superficie curva una spazialità sospesa, dove la luce penetra prevalentemente da due grandi vetrate trapezoidali che assecondano l’andamento dei telai, mentre la parete di fondo, orientata a sud, rimane sostanzialmente cieca incorporando la protuberanza esterna della casa del custode. Solo in alto viene concessa una serie di piccole feritoie orizzontali che tagliano la massa muraria la cui particolarità risiede nello sguancio obliquo che direziona la luce riflettendola sulla volta senza creare abbagliamenti; l’illuminazione artificiale, rigorosamente a incasso, è un cielo stellato (Baratelli 2019, 130) [Fig. 6].
La sperimentazione del nastro e l’importanza del colore

7 | Scuola di Matematica, aula da disegno, piano terra, 1935 (da Mornati 2002).

8 | Scuola di Matematica, aula da disegno, piano primo, 1935. Foto Vasari, FRP, BST, UniFi, busta 87, 87.24.

9 | Scuola di Matematica, scala di accesso alla biblioteca e atrio della torre delle aule (foto G. Baratelli).

10 | Scuola di Matematica, particolare dell’atrio principale (foto G. Baratelli).
Scarsa attenzione è stata rivolta dalla critica allo studio delle aule da disegno, eppure l’anomalia di forma nonché alcune scelte compositive così come di dettaglio fanno di questi ambienti un interessante episodio ancora da indagare. Le quattro aule distribuite su due piani sono pensate come grandi campate curve suddivise al centro da una sequenza di colonne; in questi spazi di lavoro, per cui è solitamente richiesta un’illuminazione costante come negli atelier, la luce si diffonde attraverso alte finestrature e lunghi nastri contrapposti interagendo con l’esterno e con il deambulatorio tramite un sottile diaframma murario.
Un documento di cantiere attesta che l’impegno di Ponti nel mettere a punto la soluzione progettuale deve essere stato notevole se per “esigenze architettoniche” (Verbale nuovi prezzi del 25 maggio 1935, UNIRM1, CERUR, busta 4, fasc. 42) durante la costruzione sono state apportate modifiche significative ad una struttura in un primo tempo molto più massiva. Alla spina centrale delle colonne corrispondevano infatti spessi setti murari a suddividere nettamente e in modo piuttosto convenzionale il servente dal servito, ma già dal 1934 – e più tardi nella versione costruita – la separazione veniva ridotta al minimo quasi a voler smaterializzare il muro (Baratelli 2019, 152).
Questa scelta non deve essere considerata pura necessità funzionale, al contrario vi si può leggere tra le righe uno dei primi esiti di una ricerca tutta personale intessuta intorno a temi decisamente moderni: la finestra a filo di facciata e la leggerezza del muro.
Occorre osservare che il nastro per Ponti non rappresenta in quegli anni una priorità, infatti l’architetto milanese lo “sfodera” quasi unicamente in questa occasione e in modo molto circoscritto se si esclude lo stabilimento Italcima a Milano progettato proprio in quegli anni con Luciano Baldessarri di cui tuttavia rifiuta parzialmente la paternità (Irace, 1986, 80-93). Qui la finestra in lunghezza si ripete ossessivamente per tutti i piani e, come ricorderà Pagano qualche anno dopo, “tutte le cadenze di finestre orizzontali a lungo metraggio, lo schema a pilastratura e il ritmo delle balconate a ordini sovrapposte e ad ampio svolgimento” (Pagano [1937] 2008, 152) sono diretta derivazione di una struttura a scheletro.
L’elemento sintattico nella Scuola di Matematica, rispetto a quella traduzione forse un po’ troppo meccanica di un principio razionalista, contribuisce piuttosto in modo del tutto inedito a creare le condizioni di una luce diffusa ideale per gli ambienti di lavoro delle sale da disegno. Ponti infatti dispone i nastri insolitamente su superfici curve preservando una continuità volumetrica all’esterno e inseguendo con la forma l’iter del sole i cui raggi possono filtrare attraverso il vetro opalino [Fig. 7]. Un principio, quello del filo di facciata, che troverà seguito anche nel progetto per gli Uffici della Montecatini (1935-1938) e che il maestro esplicherà molto più tardi in Amate l’architettura:
Con la finestra a filo (che riflette il cielo, e il correre delle nubi e il giro del sole) il buco, il vuoto, è scomparso, esiste un piano solo e solo il pieno, l’architettura è solo il pieno, volume integrale: e l’architettura è un cristallo, qua opaca e là trasparente (Ponti [1957] 2010, 140).
Neppure il posizionamento del nastro rispetto alla struttura è dato per scontato, mentre verso l’esterno l’infisso a filo di facciata è inscritto entro un telaio leggero, sul lato della corte le colonne sono arretrate e quindi tangenti al diaframma vetrato. Un tipo di ambiguità che si ritrova anche nel Le Corbusier degli anni Venti dove – come sottolinea Bruno Reichlin – il nastro conosce due diverse declinazioni: tra piedritto e piedritto (nei primi progetti puristi e in Maison La Roche) e con struttura arretrata (in casa Stein) (Reichlin 2013, 114); Ponti le comprende entrambe in uno stesso ambiente a conferma della natura fortemente sperimentale di questo spazio [Fig. 8].
La continuità anche visiva connettivo/aule da disegno era originariamente accentuata da un altro espediente tipicamente pontiano, quello del colore, che non è più apprezzabile nella sua totalità per gli stravolgimenti che l’edificio ha subito negli ultimi decenni.
L’intonaco Terranova rosso del soffitto, contrapposto al verde delle colonne, ha una funzione tutt’altro che decorativa: a partire dall’atrio guida tutte le percorrenze interne alla U dell’anello centrale e prosegue risalendo negli intradossi delle scale; in altri termini per dirla alla Ponti “intona” gli interni. Così scrive nel 1933:
Anche il soffitto deve intervenire nel gioco [del colore]: non ha affatto da essere soltanto bianco avorio: molti colori gli si confanno, dal rosso fuoco al blu carta da zucchero (Ponti 1933 a [2011], 37).
Ma il richiamo è anche ai toni schietti “all’uso antico” (Ponti 1933 b, 25) [Fig. 9]. Intorno all’intonazione dei rapporti cromatici è riconoscibile una pratica a cui egli si dedica a più riprese giungendo addirittura a ipotizzare tabelle parametriche per uno stesso ambiente domestico:
Voi potete infatti intonare stupendamente un ambiente su due, su tre colori. Giallo oro e bruno intenso; grigio argento e blu cenere; bianco e rosso; bianco e verde; […] I corridoi siano chiarissimi […]. Un colore domini e sia l’accento di ogni ambiente: il passaggio dall’uno all’altro sia gradevole e invitante, la veduta d’infilata degli ambienti attraverso le porte aperte componga essa stessa un gioco di colori, un quadro (Ponti 1933a, 40).
In effetti non solo il rosso, ma anche il verde, il nero o il grigio, ricorrono in tutto l’edificio assolvendo di volta in volta il compito di collegamento o separazione, apertura o chiusura, accentuando fenomeni percettivi. Nell’atrio in particolare gli esiti sono sorprendenti: l’ambiente quadrangolare dal soffitto rosso interamente rivestito su tre lati di bianco Carrara, trova conclusione nei due volumi gemelli in marmo nero che rinserrano i collegamenti verticali. Questo dettaglio materico produce visivamente uno sfondamento contribuendo a incanalare meglio l’occhio verso l’obiettivo della corte che si intravede dalla grande apertura al centro, un espediente scenografico che potenzia le qualità spaziali proprio dove il percorso ha inizio (Bardati 2003,176) [Fig. 10].
La biblioteca, tra reinvenzione e ‘spettacolo’ dell’architettura
Il nucleo principale dell’edificio – impostato su un impianto dalle proporzioni allungate di 1:4 – è un parallelepipedo di circa 16 x 36 x 20 metri che oltre all’atrio di ingresso include le aule di matematica pura, le sale dei professori, la grande biblioteca. I rapporti esterni sono in parte condizionati dalle direttive che Piacentini ha stabilito per il piano generale che vincolano le corrispondenze planimetriche tra i corpi di fabbrica nonché il loro aspetto in termini di aperture e di immagine (uso di materiali regionali, intonazione dei prospetti a mattoni gialli e travertino trattato a masse, finestre rettangolari nei rapporti di 1:1,5...) (Piacentini, [1932] 1986, 46). È un dato di fatto che Ponti, sia nella concezione dell’involucro che nella composizione dei pieni e dei vuoti, “svicoli” abilmente da queste indicazioni.

11 | Scuola di Matematica, prospetto sulla Piazza della Minerva (foto di G. Baratelli).
L’uso del rivestimento in travertino che dalle ultime versioni di progetto avvolge interamente il solo volume di testa, risponde probabilmente alla necessità di mantenere una continuità di fronti tra gli altri edifici più importanti prospicienti la piazza della Minerva (sulle diverse fasi di elaborazione della facciata, a intonaco, in litoceramica e in travertino, v. Mornati 2002, 58-64; sulle diverse scelte progettuali di Piacentini, Michelucci e Ponti inerenti il tema del rivestimento, v. Baratelli 2019, 177). Ponti però costruisce per sé un’immagine volumetrica completamente astratta, di un’astrattezza materica e non puramente geometrica; il rivestimento è qui una maschera omogenea costituita da lastre quadrangolari a giunto strettissimo, il cui montaggio a griglia ortogonale schiva ogni forma di direzionalità e il cui taglio singolarmente in falda crea effetti nuovi, come il “marmo tempesta” che verrà utilizzato negli uffici della Montecatini – secondo un principio poi assunto a massima:
Fate tagliare i massi controverso, inventate nuovi marmi come ho inventato il Tempesta per la Montecatini [...] il marmo lo adoperate come rivestimento mettetelo sempre in modo non costruttivo mai così [muratura isodoma] ma così [in diagonale o a 45°] o così [secondo quadrati] (Ponti [1957] 2010, 150).
Con ciò si dichiara esplicitamente il gioco del rivestimento negando riferimenti costruttivi con il muro, tutto a vantaggio della Kunstform dell’edificio. Le lastre della “placcatura” fanno parte di un disegno complessivo dove l’unico ornamento (a parte la scritta in anticorodal e la vetrata artistica) è la proprietà del materiale che si stratifica sul muro nascondendolo totalmente e creando un motivo nuovo [Fig. 11].
In questo approccio, che pure accomuna diverse architetture italiane del periodo, Ponti sembra guardare più nello specifico alla scuola viennese. Wagner, Hoffmann, Loos avevano dato luogo a interpretazioni diverse del principio tessile semperiano con soluzioni di facciata antitettoniche dalle ricche potenzialità espressive, (tra i numerosi studi sull’argomento, v. Gargiani 2004, 55-100) . Da Casa Laporte in via Brin (1935-1938) agli Uffici della Montecatini (1936-1951), alla meno nota Palazzina Duse (1939-1940), sono diverse le occasioni in cui Ponti sembra trarre liberamente interessanti spunti da questo repertorio anche se senza esplicitamente dichiararlo (sui rapporti tra Gio Ponti e Vienna v. Miodini 2001, 51-54, 65,69-72, 76).
La disposizione delle finestre che si sovrappone a questo progetto di superficie è organizzata secondo due diversi registri compresi proporzionalmente in una fascia omogenea pari a cinque lastre slittata rispetto al pattern dell’insieme; bucature rettangolari insolitamente alte al piano terreno combinano la funzione di illuminare gli ambienti di matematica pura (esposti a nord) con quella estetica di cadenzare il blocco attraverso un medesimo ritmo ripetuto che trova un completamento nelle aperture di altezza relativamente ordinaria corrispondenti al primo piano.
La separazione tra i due registri anticipa sommessamente la presenza di un’importante discontinuità; l’uniformità è presto interrotta dall’alto portale, unico elemento che si deve realmente distinguere. Il taglio nella muratura dal profondo sguancio, posto in asse rispetto al fronte, incide la massa muraria preannunciando il grande accadimento della biblioteca. La ripartizione interna dell’apertura gioca un ruolo determinante perché questo imponente volume sembra gravare sull’accesso binato dell’atrio invertendo il rapporto pieni-vuoti e sovvertendo l’ordine con cui convenzionalmente il vestibolo ostenta tutta la sua monumentalità.
Il coronamento in cemento bocciardato, che si percepisce da sotto in su simile a una trina o a una merlatura e che contrasta particolarmente con lo sviluppo quasi monolitico del blocco, costituisce la conclusione e contemporaneamente ribadisce la compattezza del corpo biblioteca segnando la quota dove l’architettura finisce e assecondando, come in altre opere di Ponti, l’antica tradizione compositiva del palazzo.
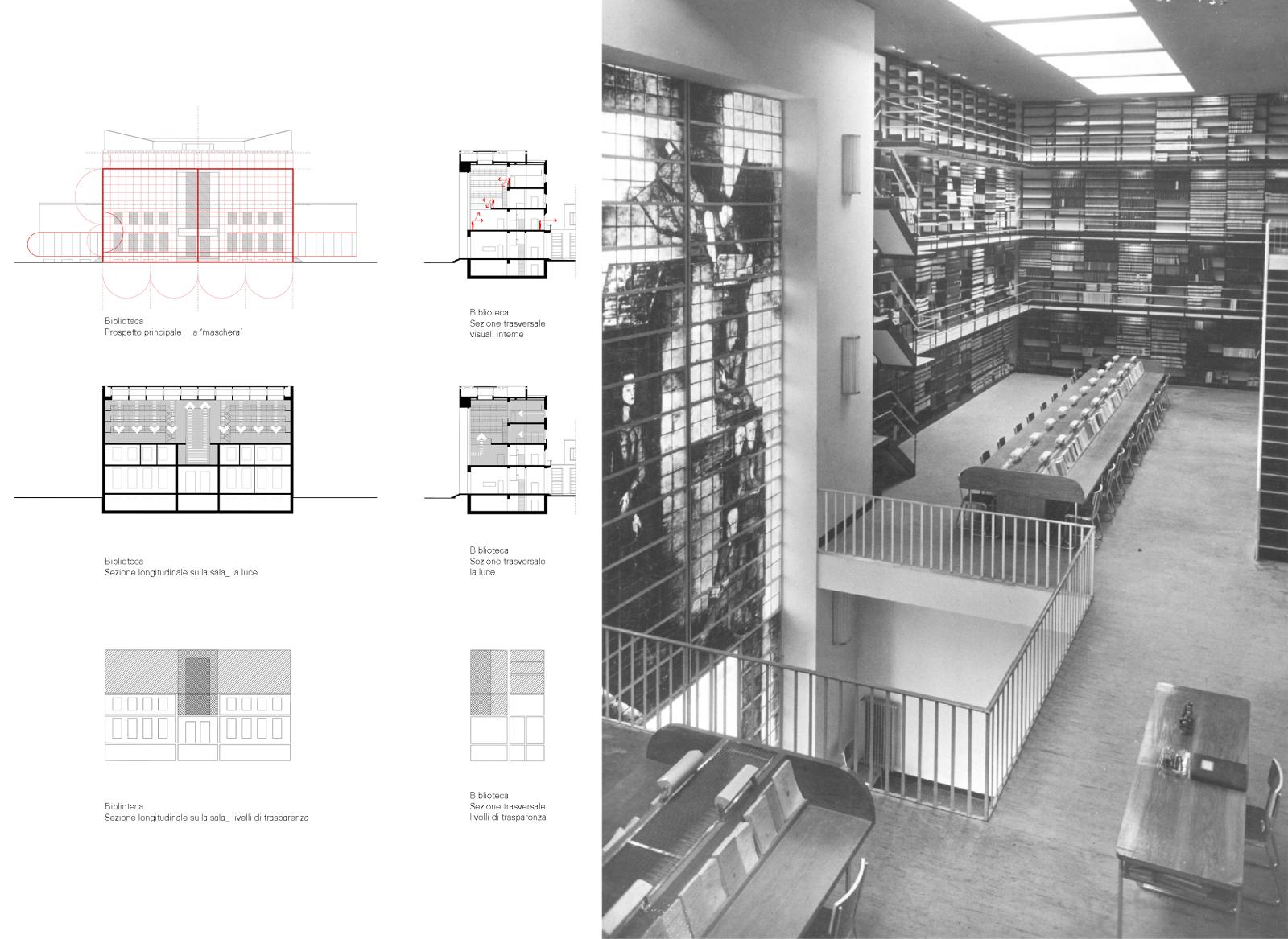
12 | Biblioteca della Scuola di Matematica, elaborati di sintesi: (in alto) prospetto principale dove si evidenzia il rapporto tra aperture e rivestimento, sezione trasversale con indicazione delle visuali interne; (al centro) sezione longitudinale e trasversale sulla biblioteca con schema del sistema ‘selettivo’ delle sorgenti luminose; (in basso) i diversi livelli di profondità dello spazio e loro sovrapposizione in corrispondenza della doppia altezza (disegni di G. Baratelli).
Scuola di Matematica, sala principale della biblioteca (da Mornati 2002).
Se si osserva l’interno, la Torre dei libri, le cui pareti sono interamente rivestite da più livelli di scaffalature metalliche perfettamente integrate, è un ambiente alto circa otto metri corrispondente ai due piani retrostanti che comunica con l’esterno solo attraverso la lunga asola centrale aperta sul fronte principale. Alla grande sala si giunge dal secondo piano attraversando un corpo retrostante significativamente più basso che comprende i depositi e stanze per la lettura, un alto muro isola chiaramente questi spazi piuttosto compressi ma ben proporzionati. Un lucernario in vetrocemento attraversa l’intera aula in lunghezza illuminando le postazioni destinate allo studio attraverso una suddivisione in due zone simmetricamente separate da una porzione cieca al centro. A questa pausa corrispondeva in origine il grande buco nel solaio da cui era possibile affacciarsi sull’atrio dei professori proprio davanti al portale di ingresso che incorniciava una vetrata policroma. L’inserimento dell’opera, realizzata su disegno dello stesso Ponti e probabilmente con l’aiuto di Pietro Chiesa per Fontana Arte (Falconi, 2005, 74) rispondeva a una seconda tacita priorità: quella di favorire una integrazione completa tra arte e architettura innescando una serie di dinamiche interne e offrendo diversi punti di osservazione capaci di sollecitare la normale psicologia della percezione di un soggetto in movimento [Fig. 12].
Il muro interno si sarebbe configurato come uno schermo permeabile secondo una estetica che si combinava all’occorrenza con esigenze di controllo dell’intera “macchina”: attraverso due scale simmetriche e una serie di piccole aperture lo studioso o il bibliotecario avevano accesso agli spazi più raccolti dei depositi e posizionandosi in corrispondenza del centro della sala avrebbero trovato nel balcone interno una postazione privilegiata, da qui la vista si sarebbe direzionata verso l’importante traguardo ottico della vetrata, per poi soffermarsi agilmente sulla sala stessa e sull’atrio al piano inferiore, dove in un gioco di rimandi gli stessi docenti avrebbero potuto apprezzare la grande sala da sotto in su e in tutta la sua grandezza. Il diaframma della vetrata retroilluminata attraverso i suoi colori avrebbe poi ricreato le suggestioni della campata di una cattedrale, cosa alquanto inusuale per una biblioteca.

13 | Biblioteca della Scuola di Matematica, affaccio interno sulla sala di lettura. Allo stato attuale l’atrio dei professori non è più visibile dalla sala principale (foto di G. Baratelli).
Si arriva così alla costruzione di uno spazio giocato su più livelli di profondità: il volume della sala a doppia altezza, lo schermo murario che con le aperture assiali costituisce una seconda facciata interna e il vuoto centrale dell’atrio professori che genera una zona neutra di interferenza o di trasparenza nella sua accezione fenomenica, cioè quella particolare condizione per cui “si vedono due o più figure sovrapposte e ognuna di esse rivendica per sé la parte sovrapposta comune” (Rowe, Slutzky, 1997, 22). Le scale, gli affacci, le porte interne e la vetrata animata sono a loro volta parti di un lessico che contribuisce alla definizione di una architettura estremamente seduttiva per chi la vive e la attraversa [Fig. 13].
Pare legittimo domandarsi a questo punto quali possano essere i riferimenti di questa spazialità oltre che i particolari dispositivi di cui l’architetto si serve.
Nuove biblioteche dal carattere dichiaratamente moderno costituivano all’epoca in Europa episodi sporadici, fatta eccezione per la Biblioteca civica di Asplund (1920-1928), grande monumento urbano di Stoccolma, quella cantonale di Berna (1928-1931) dall’impianto distributivo articolato o la Cambridge Library di Giles Gilbert Scott (1931-1934), torre-deposito simile in termini tipologici a quella che Piacentini avrebbe dovuto costruire nella Città Universitaria. Più in generale la biblioteca di nuova concezione pensata a servizio degli istituti superiori si identificava in un edificio a essa interamente dedicato, per lo più isolato e dotato di un grande ambiente per la lettura su cui affacciavano i depositi come era tipico dei campus statunitensi (Carbonara 1941,246-247); ovvero, in alternativa, era costituita semplicemente da una serie di ambienti contigui contenuti nel nucleo compatto del corpo di fabbrica e completamente privi di visibilità dall’esterno, scelta intrapresa anche dai colleghi architetti nella Città Universitaria rispetto alla quale la Scuola di Matematica si distingue.
Il principio su cui è costruito lo spazio interno di Ponti trova fondamento su qualcosa di più antico: l’archetipo della biblioteca foderata da libri organizzati su più scaffalature collegate da scale. Ma la tradizione dello Saalsystem che solitamente coincideva, salvo eccezioni, con un ambiente poco areato con possibilità di essere illuminato solo dall’alto, viene totalmente reinventata da Ponti che ne fa uno spazio moderno e vivibile moltiplicando le sorgenti luminose attraverso cui la luce viene riflessa, rifranta, filtrata secondo gradi di specializzazione diversi che contribuiscono a evidenziare gli ambiti funzionali con un’alternanza di zone in luce e in ombra (Baratelli 2019, 147-148). I coups de théâtre degli affacci interni e una certa sacralità accresciuta dalla presenza della vetrata policroma – autentica dimostrazione di “arte pubblica” come saggio di bravura del Ponti artista – rendono l’ambiente unico.
La grande sala di lettura è forse anche l’occasione per iniziare a studiare sezioni sempre più articolate – o meglio animate – e, nonostante gli elaborati grafici superstiti piuttosto scarni, nella Scuola di Matematica si può intravedere il germe di una pratica compositiva incentrata su traguardi visivi che trova continuità nel lavoro dell’architetto.

14 | Palazzo Liviano, l’atrio prima di essere affrescato, 1939. Archivio Generale di Ateneo, Archivio dei Consorzi edilizi, b. 143 fasc. Ponti, su Concessione dell’Università degli Studi di Padova, Ufficio Gestione documentale.
Nel progetto per il Palazzo della Facoltà di Lettere di Padova, esito di un concorso nazionale del 1934, l’architetto, che probabilmente è anche divertito da un incarico in cui è chiamato a collaborare con un artista, cosa a lui particolarmente congeniale, presenta due soluzioni per il vestibolo di ingresso. Nella proposta realizzata l’atrio assume un ruolo centrale che in parte supplisce l’assenza di una corte; è uno spazio a tutta altezza a cui si accede frontalmente salendo pochi gradini da un profondo portale a più fornici e dove la salita è preparatoria allo “spettacolo interno”; qui l’occhio è catturato dalla scala di accesso al Museo di Archeologia, un sistema di rampe con andamento a zig zag, che negli schizzi è raffigurato brulicante di figure affacciate sul vuoto [Fig. 14].
Ogni lato è occupato da un accadimento che introduce nuovi piani prospettici, la sola parete opposta all’ ingresso è nuda in quanto assume il ruolo di fondale. Se nella Scuola di Matematica l’osservatore ha come traguardo visivo la vetrata al centro, nel Liviano (come rivelano alcune brevi annotazioni d’intenzione) il quadro è costituito dal muro su cui campeggerà il grande affresco di Campigli (Miodini 2001, 152-157). Un’intenzione scenica che sintetizza efficacemente Lisa Ponti:
L’atrio è in posizione centrale, sostituisce il portico (o la corte) per la sosta degli studenti. Ha un gioco di rampe e balconate, in luogo dell’usuale ‘scalone’: campigliescamente affollato, ai diversi livelli, fa delle cerimonie uno spettacolo (Licitra Ponti 1990, 92).
La preoccupazione di far confluire in un unico ambiente principale spazi secondari, pur con le dovute differenze, interessa inizialmente parte del filone domestico di Ponti tra gli anni Venti e Trenta. Nella Casa Bouilhet a Garches realizzata con Lancia (1925-1926), la hall centrale è organizzata su due livelli, tutti gli altri ambienti sono disposti intorno e collegati da un camminamento in quota accessibile attraverso una lunga scala a vista. In generale la hall diventa oggetto di osservazione per alloggi speciali in cui il programma è più libero perché destinato a una élite, esempi lontani dalle “case tipiche” progettate in ambito urbano dal contesto già determinato, ma residenze isolate che trovano una formalizzazione concreta nel Ponti pubblicista. Come sottolinea lo stesso architetto in un articolo del 1934:
Per godere la campagna, [la casa] se a due piani può svolgersi ingegnosamente intorno alla scala con divertenti prospettive e la sala del soggiorno essere alta magari due piani e con le stanze che si aprono in modo pittoresco (Ponti [1934b] 2011, 70).
Di nuovo nell’alloggio-studio il vano centrale alto due piani con balconata è una possibile risorsa che arricchisce percettivamente l’ambiente di piacevoli vedute “da sopra” e “da sotto”, un “bel finestrone” fa il resto (Ponti [1934a] 2011, 60). Un tema che trova forse la sua formalizzazione più raffinata nella Casa Laporte dove Ponti dimostra di voler rompere la monotonia dei livelli e di saper elaborare piante sempre più dinamiche, in cui “il salone consente di essere guardato dall’alto” dando “un respiro ed un ordine tutto nuovo” (Ponti 1937, 2-11).
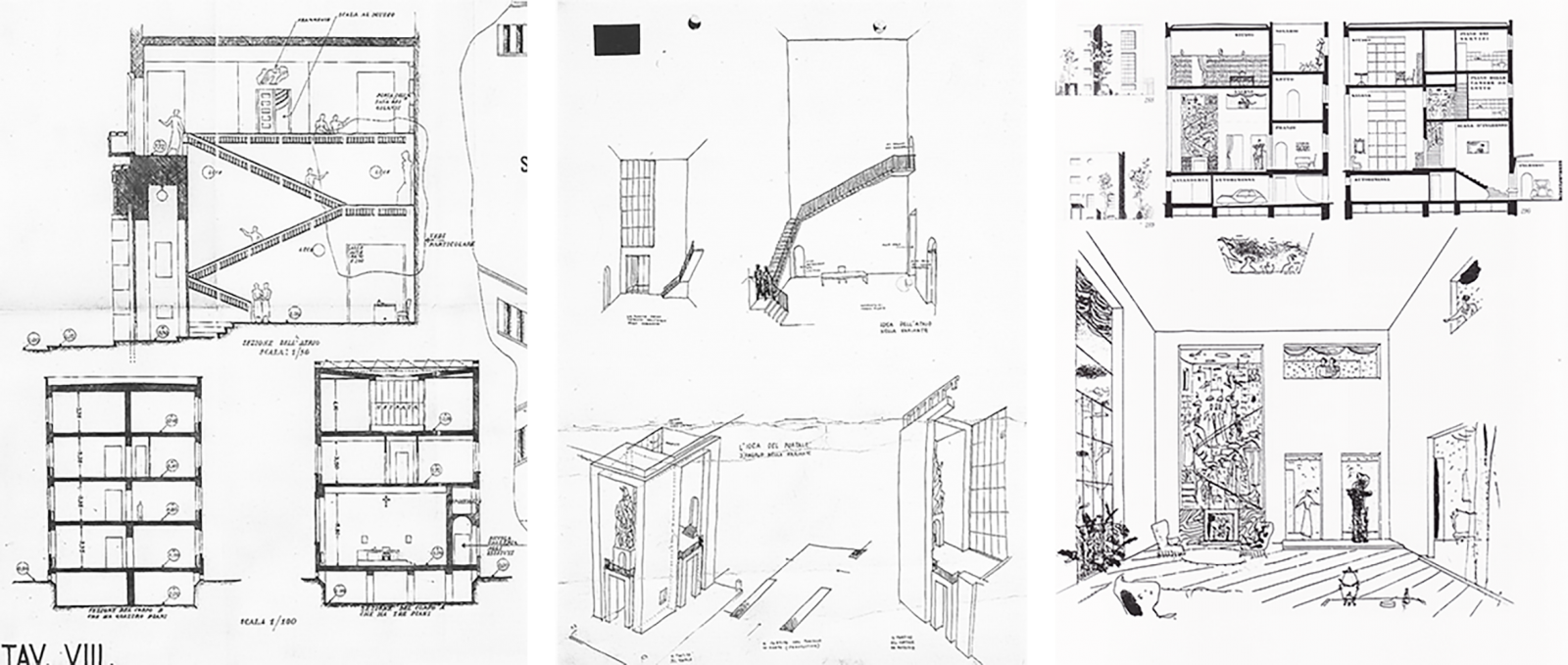
15 | G. Ponti, Palazzo della Facoltà di Lettere della R. Università di Padova in piazza Capitaniato, sezione dell’atrio, s.d. (ca.1934) (da Miodini 2001).
Palazzo della Facoltà di Lettere, Il Liviano, schizzo s.d., ca.1934 (da Miodini 2001).
G. Ponti, Progetto di villa in città per un uomo d’affari in via Claudiano a Milano, prospetti, sezioni e veduta interna pubblicati in “Stile”, 1941 (da La Pietra 1995).
Ad un certo punto la ricerca di un’articolazione spaziale non sembra più essere solamente una peculiarità dell’ambiente domestico. La vetrata, le scale e il ballatoio o l’affaccio interno diventano sofisticati episodi parte di una sequenza prospettica e di una visione cinestetica dello spazio che nel tempo deve aver portato a superare le barriere dei “generi”; così nei disegni di sezione della Casa per un uomo d’affari, pubblicata su “Stile” nel 1941, è possibile riconoscere la sovrapposizione di figure e temi provenienti dalla Biblioteca di Matematica come dal Liviano. Ne scrive lo stesso Ponti:
L’ingresso è come io vagheggio, piccolo, discreto, senza troppe pretese […] da questo ingresso si sale per una comoda scala tra le mura [e si raggiunge] il cuore della casa […] il salone è qui il gran colpo […] essendo alto un piano e mezzo consente che dalla galleria superiore si apra una finestra interna, cosa piacevole da vedere dal basso (specie se animata) e punto di vista bellissimo per guardare dall’alto (Ponti [1941] 1995, 135) [Fig. 15].
A distanza di anni l’architetto, con lo spirito dissacrante e autoironico che gli è proprio, rivedrà in modo critico sulla rivista “Stile” il comporre per volumi o per ‘cuboni’ – tipico del palazzo storico o del monumento – così come la maniera moderna di costruire edifici “indefiniti sia in altezza che in lunghezza” quindi ripetitivi, teoricamente illimitati nonché lontani da ogni aspirazione artistica, ammettendo il limite del muro e delle sue partizioni quasi evocando la dissoluzione del limite fisico della parete rispetto allo spazio:
La costruzione parli e si determini, si dichiari. Giacché procedo per episodi, un episodio perenne che mi piace confessare, è quello del ‘rifare per me’ tutte le mie architetture: subito appena finito l’edificio della Matematica all’Università di Roma, io ho capito che la parte superiore chiusa (biblioteca illuminata dall’alto) io dovevo farla vedere (spettacolo vivo) in facciata. Questo spettacolo di vita, questa espressione sostanziale dell’architettura, questo suo passare da un accademismo ermetico ad una dichiarazione di sé, è ciò che più mi muove (Ponti 1944, 1) [Fig. 16].
16 | G. Ponti, Copertina di “Stile” 39 (1944).
G. Ponti, Verso lo spettacolo dell’architettura. “Stile” 39, 1944.
Indipendentemente da questa paradossale presa di posizione, il fascino della Scuola di Matematica risiede nel suo essere architettura di transizione nel pensiero e nell’opera dell’autore tra un prima in cui l’interesse prevalente è stato catturato dalla ricerca di un linguaggio e un dopo che coincide con il periodo di maturazione degli anni Trenta.
Anche volendo distinguere tra l’invenzione pura della torre delle aule e della U di collegamento e la reinvenzione di uno spazio, quello della biblioteca, è nella contraddittorietà apparente tra esterno e interno che il lavoro di Ponti sembra trovare una felice sintesi: l’esterno è il regno delle forme pure concepite geometricamente come inestensibili e dunque forme d’arte autentiche che non accettano variazioni dal cui equilibrio e dalla cui opposizione nasce l’insieme, un insieme di volumi statici come monumenti, “la cupola […] sfera troncata e svuotata che poggia, buccia di mezza sfera, l’anello d’un circo, d’un teatro” (Ponti [1957] 2010, 48), architettura fatta di “monotipi” di pezzi unici definiti a priori come “il Partenone, il Battistero, la Rotonda di Palladio”, ma anche un insieme di analogie e rimandi agli elementi urbani primari del palazzo e della piazza italiana, della torre scenica di un teatro. L’interno invece è il teatro stesso quindi il luogo degli accadimenti funzionali e percettivi, spazio dinamico della vita, funzione sublimata ad arte con cui Ponti cerca di “incantare”, come lui stesso dichiara, il fruitore e che forse ci spinge ancora a percorrere e rileggere, pur con piedi ben piantati per terra, questo edificio:
L’architettura-arte è utile e funziona anche su un altro piano, quello per “guardarla”, quello dell’arte, quello di incantarci e raggiungere, in poetica, le lettere, la musica, la pittura, che non hanno altra utilità o funzione – ma quale! – che quella di incantarci, dopo aver incantato chi le creò (Ponti [1957] 2010, 75).
Bibliografia
- Architettura 1935
“Architettura”, speciale (1935), 45-50. - Baratelli 2019
G. Baratelli, La Città Universitaria di Roma. Costruzione di un testo architettonico, Milano 2019. - Bardati 2003
F. Bardati, La Scuola di Matematica di Gio Ponti: i materiali e la qualità dello spazio, in V. Franchetti Pardo (a cura di), L’architettura nelle città italiane del XX secolo, Milano 2003, 175-181. - Carbonara 1941
P. Carbonara, Compiti e caratteri della biblioteca moderna, “Architettura” 6 (1941), 237-248. - Cerutti Fusco 2003
A. Cerutti Fusco, La Scuola di Matematica nella Città Universitaria di Roma: opera dei primi anni Trenta di Giovanni (Gio) Ponti (1891 - 1979); alcune riflessioni, in V. Franchetti Pardo (a cura di), L’architettura nelle città italiane del XX secolo, Milano 2003, 103-120. - Ciucci 1989
G. Ciucci, Lo stile di Libera, in G. Belli, V. Gregotti et al. (a cura di), Adalberto Libera. Opera Completa, Milano 1989, 62-79. - Falconi 2005
L. Falconi, Gio Ponti, interni, oggetti, disegni (1920-1976), Milano 2005. - Gargiani 2004
R.Gargiani, Vienna o del sublime della superficie, in G. Fanelli, R. Gargiani, Storia dell’architettura contemporanea: spazio, struttura, involucro, Bari, 2004, 55-100. - Irace 1986
F. Irace, Un esempio di architettura industriale degli anni Trenta: lo stabilimento Italcima, in O. Selvafolta (a cura di), Costruire in Lombardia 1880 - 1980, Milano 1986, 80-93. - La Pietra 1995
U. La Pietra (a cura di) Gio Ponti, Milano 1995. - Licitra Ponti 1990
L. Licitra Ponti, Gio Ponti. L’opera, Milano 1990. - Miodini 2001
L. Miodini, Gio Ponti, Gli anni Trenta, Milano 2001. - Mornati 2002
S. Mornati, L’edificio della Scuola di Matematica di Giò Ponti alla Città Universitaria di Roma, “Bollettino dell’Unione Matematica Italiana” 1 (2002), 43-71. - Mornati 2020
S. Mornati, La scuola di Matematica di Roma, 1932-1935, in M. Casciato, F. Irace (a cura di), Gio Ponti. Amare l’architettura, catalogo della mostra (27 novembre 2019 – 27 settembre 2020, MAXXI), Firenze 2019, 92-95. - Pacini 1933
R. Pacini, La Città Universitaria di Roma, “Architettura” VIII (1933), 475-495. - Pagano [1937] 2008
G. Pagano, Tre anni di architettura in Italia, “Casabella” 110 (1937) in C. De Seta (a cura di), Giuseppe Pagano. Architettura e città durante il fascismo, Milano 2008, 145-154. - Piacentini [1932] 1985
M. Piacentini, Lettera ai progettisti del 12 settembre 1932, in E. Guidoni, M. Regni Sennato (a cura di), 1935/1985 - La “Sapienza” nella Città Universitaria, Roma 1985, 46. - Piacentini 1935
M. Piacentini, Metodi e caratteristiche, “Architettura”, speciale (1935), 2-8. - Ponti 1929
G. Ponti, Particolari d’architettura modernissima nelle costruzioni di Roberto Mallet-Stevens, “Domus” 2 (1929), 38. - Ponti 1932
G. Ponti, A proposito delle dimensioni degli ambienti nelle case, “Domus” 56 (1932), 457. - Ponti [1933a] 2011
G. Ponti, I colori nell’arredamento, “Corriere della sera”, 31 dicembre 1933, in L. Molinari e C. Rostagni (a cura di), Gio Ponti e il “Corriere della sera”, 1930-1963, Milano 2011, 36-40. - Ponti 1933b
G. Ponti, Colore negli ambienti, “Domus” 61 (1933), 25. - Ponti [1934a] 2011
G. Ponti, L’alloggio-studio,“Corriere della sera”, 22 febbraio 1934, in L. Molinari e C. Rostagni ( a cura di), Gio Ponti e il “Corriere della sera”, 1930-1963, Milano 2011, 58-63. - Ponti [1934 b] 2011
G. Ponti, Per godere la campagna, “Corriere della sera”, 23 marzo 1934, in L. Molinari e C. Rostagni (a cura di), Gio Ponti e il “Corriere della sera”, 1930-1963, Milano 2011, 64-70. - Ponti 1937
G. Ponti, Una villa a tre appartamenti in Milano, “Domus” 111, 1937, 2-9. - Ponti [1941] 1995
G. Ponti, Progetto per una villa in città, “Stile”, 1941, in U. La Pietra (a cura di), Gio Ponti, Milano, 1995, 134-135. - Ponti 1944
G. Ponti, Invenzione d’una architettura composta. Dai “cuboni” alla composizione d’una architettura, “Stile” 39 (1944), 1-16. - Ponti [1957] 2010
G. Ponti, Amate l’architettura, Milano [1957] 2010. - Poretti 2008
S. Poretti, Modernismi italiani, architettura e costruzione nel Novecento, Roma 2008. - Reichlin 2013
B. Reichlin, Dalla “soluzione elegante” all’“edificio aperto” Scritti attorno ad alcune opere di Le Corbusier, Milano 2013. - Rowe, Slutzky, 1997
C. Rowe, R. Slutzky, Transparency, Basel 1997. - Salvo 2015
S. Salvo, Conservation and modern architecture. Fortune and misfortune of the School of Matematics at Rome University (G. Ponti, 1932-1935), Roma 2015. - Spano 1935
N. Spano, L’Università di Roma, Roma 1935.
English abstract
The School of Mathematics (1932-1935), designed and built for the new Sapienza University in Rome, is built during a crucial moment of the professional career of the architect, who until that time had long devoted himself mainly to the design of residential projects. The civil architecture of an avant-garde university proves to be the ideal opportunity to develop and define a series of interesting compositional and constructive solutions that will become part of Ponti’s vocabulary. This short essay focuses on the genesis of the project concentrating on some key points: the role of the building in the general plan devised by Piacentini, the volumetric organization (library – courtyard – drawing rooms – auditoriums), the dynamic concept in the definition of interior space. The investigation intends also to focus on an interesting case study: the body of the library that, being characterized by a certain degree of autonomy, acts simultaneously as ‘head’ and ‘gateway’ of the whole composition. It is our intention, therefore, to explore the design aspects that form the interior architectural quality of the building: from the relationships in height, to the faces, to the multiplication of light sources, to the visual goals, and finally to question the degree of ambiguity or transparency of the ‘facade-mask’ that hides the great void of the reading room. All these elements work together to create a space that is a highly evocative “Totalkunstwerk” but also consistent with the needs of a modern library.
keywords | Gio Ponti; School of Mathematics; interior space; composition; colour.
La Redazione di Engramma è grata ai colleghi – amici e studiosi – che, seguendo la procedura peer review a doppio cieco, hanno sottoposto a lettura, revisione e giudizio questo saggio.
(v. Albo dei referee di Engramma)
Per citare questo articolo / To cite this article: Guia Baratelli, L′invenzione dello spazio nella Scuola di Matematica di Gio Ponti, “La Rivista di Engramma” n. 175, settembre 2020, pp. 75-102 | PDF dell’articolo